Do Small Animals Have A Large Surface Area To Volume Ratio

Surface surface area per unit book

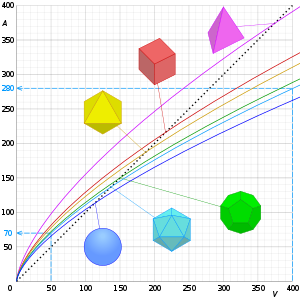
Graphs of surface area, A against volume, V of the Ideal solids and a sphere, showing that the surface expanse decreases for rounder shapes, and the surface-area-to-volume ratio decreases with increasing volume. Their intercepts with the dashed lines show that when the volume increases 8 (ii³) times, the surface area increases four (2²) times.

The surface-area-to-book ratio, also called the surface-to-volume ratio and variously denoted sa/vol or SA:5, is the amount of surface expanse per unit book of an object or collection of objects.

SA:Five is an important concept in science and engineering. Information technology is used to explain the relation between structure and function in processes occurring through the surface and the book. Skillful examples for such processes are processes governed by the rut equation,^[1] i.e., diffusion and oestrus transfer past conduction.^[ii] SA:V is used to explicate the diffusion of minor molecules, similar oxygen and carbon dioxide betwixt air, blood and cells,^[three] water loss past animals,^[four] bacterial morphogenesis,^[v] organism'due south thermoregulation,^[6] pattern of artificial bone tissue,^[vii] artificial lungs ^[eight] and many more than biological and biotechnological structures. For more examples come across Glazier.^[nine]

The relation betwixt SA:V and diffusion or heat conduction rate is explained from flux and surface perspective, focusing on the surface of a trunk as the place where improvidence, or heat conduction, takes place, i.e., the larger the SA:V at that place is more surface area per unit volume through which material can diffuse, therefore, the diffusion or heat conduction, will be faster. Similar explanation appears in the literature: "Small size implies a large ratio of surface surface area to volume, thereby helping to maximize the uptake of nutrients across the plasma membrane",^[10] and elsewhere.^{[9] [11] [12]}

For a given volume, the object with the smallest surface expanse (and therefore with the smallest SA:5) is a brawl, a consequence of the isoperimetric inequality in 3 dimensions. By contrast, objects with acute-angled spikes volition accept very big surface area for a given volume.

SA:V for assurance and northward-balls [edit]

A ball is a 3-dimensional object, being the solid version of a sphere. (In geometry, the term sphere properly refers only to the surface, so a sphere thus lacks volume in this context.) Balls exist in whatever dimension and are generically called due north-balls, where n is the number of dimensions.

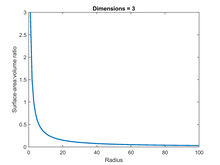
Plot of the surface-area:volume ratio (SA:V) for a iii-dimensional ball, showing the ratio reject inversely as the radius of the brawl increases.

For an ordinary 3-dimensional ball, the SA:5 tin be calculated using the standard equations for the surface and book, which are, respectively, ${\displaystyle four\pi {r^{2}}}$ and ${\displaystyle (4/3)\pi {r^{3}}}$ . For the unit case in which r = 1 the SA:V is thus iii. The SA:V has an inverse relationship with the radius - if the radius is doubled the SA:V halves (see figure).

The same reasoning tin can be generalized to n-balls using the full general equations for book and expanse, which are:

volume = ${\displaystyle r^{n}\pi ^{due north/2} \over \Gamma (1+n/2)}$ ; surface expanse = ${\displaystyle nr^{n-1}\pi ^{due north/two} \over \Gamma (ane+{n/two})}$

Plot of surface-area:volume ratio (SA:V) for n-balls as a function of the number of dimensions and of radius size. Notation the linear scaling equally a function of dimensionality and the inverse scaling as a function of radius.

And so the ratio reduces to ${\displaystyle nr^{-1}}$ . Thus, the aforementioned linear relationship between surface area and volume holds for any number of dimensions (see figure): doubling the radius ever halves the ratio.

Dimension [edit]

The surface-surface area-to-volume ratio has physical dimension L⁻¹ (inverse length) and is therefore expressed in units of inverse distance. Every bit an example, a cube with sides of length i cm will accept a surface area of vi cm² and a book of 1 cm³. The surface to volume ratio for this cube is thus

${\displaystyle {\mbox{SA:5}}={\frac {six~{\mbox{cm}}^{2}}{1~{\mbox{cm}}^{3}}}=6~{\mbox{cm}}^{-1}}$ .

For a given shape, SA:V is inversely proportional to size. A cube two cm on a side has a ratio of 3 cm^−one, half that of a cube 1 cm on a side. Conversely, preserving SA:Five as size increases requires irresolute to a less compact shape.

Physical chemistry [edit]

Materials with loftier surface area to book ratio (east.chiliad. very small bore, very porous, or otherwise not compact) react at much faster rates than monolithic materials, because more surface is available to react. An instance is grain dust: while grain is not typically flammable, grain grit is explosive. Finely ground common salt dissolves much more quickly than coarse table salt.

A loftier surface area to volume ratio provides a strong "driving force" to speed upwardly thermodynamic processes that minimize free energy.

Biological science [edit]

The ratio between the surface expanse and book of cells and organisms has an enormous impact on their biology, including their physiology and behavior. For example, many aquatic microorganisms take increased surface surface area to increase their drag in the water. This reduces their charge per unit of sink and allows them to remain almost the surface with less free energy expenditure.^{[ citation needed ]}

An increased surface area to volume ratio likewise means increased exposure to the environs. The finely-branched appendages of filter feeders such as krill provide a large surface area to sift the h2o for food.^[thirteen]

Private organs like the lung accept numerous internal branchings that increment the expanse; in the example of the lung, the large surface supports gas exchange, bringing oxygen into the blood and releasing carbon dioxide from the blood.^{[14] [15]} Similarly, the pocket-size intestine has a finely wrinkled internal surface, allowing the body to absorb nutrients efficiently.^[16]

Cells can achieve a high surface expanse to volume ratio with an elaborately convoluted surface, like the microvilli lining the small intestine.^[17]

Increased surface expanse tin besides atomic number 82 to biological bug. More than contact with the environment through the surface of a cell or an organ (relative to its volume) increases loss of water and dissolved substances. Loftier surface surface area to book ratios besides present bug of temperature control in unfavorable environments.^{[ citation needed ]}

The surface to volume ratios of organisms of different sizes also leads to some biological rules such every bit Allen's rule, Bergmann'due south dominion^{[18] [19] [xx]} and gigantothermy.^[21]

Fire spread [edit]

In the context of wildfires, the ratio of the expanse of a solid fuel to its book is an of import measurement. Fire spread behavior is often correlated to the surface-expanse-to-volume ratio of the fuel (e.g. leaves and branches). The college its value, the faster a particle responds to changes in ecology conditions, such as temperature or moisture. Higher values are besides correlated to shorter fuel ignition times, and hence faster burn down spread rates.

Planetary cooling [edit]

A trunk of icy or rocky material in outer space may, if it tin can build and retain sufficient heat, develop a differentiated interior and modify its surface through volcanic or tectonic action. The length of time through which a planetary body can maintain surface-altering activity depends on how well it retains estrus, and this is governed by its expanse-to-book ratio. For Vesta (r=263 km), the ratio is so high that astronomers were surprised to find that it did differentiate and have brief volcanic activity. The moon, Mercury and Mars have radii in the depression thousands of kilometers; all iii retained heat well enough to be thoroughly differentiated although later on a billion years or and then they became as well cool to show annihilation more than very localized and infrequent volcanic activeness. As of April 2019, nevertheless, NASA has announced the detection of a "marsquake" measured on April 6, 2019, by NASA's InSight lander.^[22] Venus and World (r>6,000 km) have sufficiently depression area-to-volume ratios (roughly half that of Mars and much lower than all other known rocky bodies) so that their heat loss is minimal.^[23]

Mathematical examples [edit]

Shape		Characteristic length ${\displaystyle a}$	Surface area	Book	SA/Five ratio	SA/V ratio for unit volume
Tetrahedron		edge	${\displaystyle {\sqrt {3}}a^{2}}$	${\displaystyle {\frac {{\sqrt {2}}a^{three}}{12}}}$	${\displaystyle {\frac {6{\sqrt {6}}}{a}}\approx {\frac {fourteen.697}{a}}}$	7.21
Cube		edge	${\displaystyle 6a^{2}}$	${\displaystyle a^{3}}$	${\displaystyle {\frac {half-dozen}{a}}}$	half dozen
Octahedron		edge	${\displaystyle 2{\sqrt {3}}a^{2}}$	${\displaystyle {\frac {one}{3}}{\sqrt {ii}}a^{3}}$	${\displaystyle {\frac {3{\sqrt {6}}}{a}}\approx {\frac {seven.348}{a}}}$	5.72
Dodecahedron		edge	${\displaystyle three{\sqrt {25+ten{\sqrt {v}}}}a^{two}}$	${\displaystyle {\frac {1}{4}}(15+7{\sqrt {five}})a^{3}}$	${\displaystyle {\frac {12{\sqrt {25+10{\sqrt {five}}}}}{(15+7{\sqrt {v}})a}}\approx {\frac {two.694}{a}}}$	v.31
Capsule		radius (R)	${\displaystyle 4\pi a^{two}+2\pi a\cdot 2a=8\pi a^{2}}$	${\displaystyle {\frac {4\pi a^{3}}{3}}+\pi a^{2}\cdot 2a={\frac {10\pi a^{3}}{3}}}$	${\displaystyle {\frac {12}{5a}}}$	5.251
Icosahedron		edge	${\displaystyle five{\sqrt {3}}a^{2}}$	${\displaystyle {\frac {5}{12}}(three+{\sqrt {5}})a^{3}}$	${\displaystyle {\frac {12{\sqrt {3}}}{(3+{\sqrt {5}})a}}\approx {\frac {three.970}{a}}}$	5.148
Sphere		radius	${\displaystyle four\pi a^{ii}}$	${\displaystyle {\frac {iv\pi a^{iii}}{3}}}$	${\displaystyle {\frac {3}{a}}}$	4.83598

Examples of cubes of different sizes

Side of cube	Side2	Area of a single face	6 × side2	Area of entire cube (6 faces)	Side3	Book	Ratio of area to volume
2	2x2	4	6x2x2	24	2x2x2	8	3:1
4	4x4	xvi	6x4x4	96	4x4x4	64	3:2
half-dozen	6x6	36	6x6x6	216	6x6x6	216	3:3
8	8x8	64	6x8x8	384	8x8x8	512	3:4
12	12x12	144	6x12x12	864	12x12x12	1728	3:six
20	20x20	400	6x20x20	2400	20x20x20	8000	three:10
50	50x50	2500	6x50x50	15000	50x50x50	125000	three:25
1000	1000x1000	million	6x1000x1000	6000000	1000x1000x1000	1000000000	three:500

Run into too [edit]

• Compactness measure of a shape
• Dust explosion
• Square–cube police
• Specific surface area

References [edit]

• Schmidt-Nielsen, Knut (1984). Scaling: Why is Animal Size so Important? . New York, NY: Cambridge University Printing. ISBN978-0-521-26657-4. OCLC 10697247.
• Vogel, Steven (1988). Life'due south Devices: The Physical World of Animals and Plants. Princeton, NJ: Princeton University Press. ISBN978-0-691-08504-3. OCLC 18070616.

Specific

1. ^ Planinšič, Gorazd; Vollmer, Michael (February 20, 2008). "The surface-to-volume ratio in thermal physics: from cheese cube physics to animate being metabolism". European Journal of Physics. 29 (2): 369–384. Bibcode:2008EJPh...29..369P. doi:10.1088/0143-0807/29/2/017. Retrieved 9 July 2021.
2. ^ Planinšič, Gorazd (2008). "The surface-to-volume ratio in thermal physics: from cheese cube physics to animal metabolism". European Journal of Physics European Physical Guild, Find Out More. 29 (2): 369–384. Bibcode:2008EJPh...29..369P. doi:10.1088/0143-0807/29/two/017.
3. ^ Williams, Peter; Warwick, Roger; Dyson, Mary; Bannister, Lawrence H. (2005). Gray'south Anatomy (39 ed.). Churchill Livingstone. pp. 1278–1282.
4. ^ Jeremy M., Howard; Hannah-Beth, Griffis; Westendorf, Rachel; Williams, Jason B. (2019). "The influence of size and abiotic factors on cutaneous water loss". Advances in Physiology Education. 44 (3): 387–393. doi:10.1152/advan.00152.2019. PMID 32628526.
5. ^ Harris, Leigh Thou.; Theriot, Julie A. (2018). "Surface Surface area to Volume Ratio: A Natural Variable for Bacterial Morphogenesis". Trends in Microbiology. 26 (10): 815–832. doi:10.1016/j.tim.2018.04.008. PMC6150810. PMID 29843923.
6. ^ Louw, Gideon North. (1993). Physiological Animal Environmental. Longman Pub Group.
7. ^ Nguyen, Thanh Danh; Olufemi East., Kadri; Vassilios I., Sikavitsas; Voronov, Roman S. (2019). "Scaffolds with a High Surface Area-to-Volume Ratio and Cultured Under Fast Flow Perfusion Event in Optimal O2 Delivery to the Cells in Artificial Bone Tissues". Applied Sciences. 9 (11): 2381. doi:ten.3390/app9112381.
8. ^ J. K, Lee; H. H., Kung; L. F., Mockros (2008). "Microchannel Technologies for Bogus Lungs: (one) Theory". ASAIO Journal. 54 (four): 372–382. doi:10.1097/MAT.0b013e31817ed9e1. PMID 18645354. S2CID 19505655.
9. ^ ^{a b} Glazier, Douglas Southward. (2010). "A unifying explanation for diverse metabolic scaling in animals and plants". Biological Reviews. 85 (1): 111–138. doi:x.1111/j.1469-185X.2009.00095.x. PMID 19895606. S2CID 28572410.
10. ^ Alberts, Bruce (2002). "The Diverseness of Genomes and the Tree of Life". Molecular Biology of the Cell, fourth edition. New York: Garland Scientific discipline. ISBN0-8153-3218-1. ISBN 0-8153-4072-9.
11. ^ Adam, John (2020-01-01). "What's Your Sphericity Index? Rationalizing Area and Volume". Virginia Mathematics Instructor. 46 (2).
12. ^ Okie, Jordan Thousand. (March 2013). "General models for the spectra of surface surface area scaling strategies of cells and organisms: fractality, geometric dissimilitude, and internalization". The American Naturalist. 181 (3): 421–439. doi:10.1086/669150. ISSN 1537-5323. PMID 23448890. S2CID 23434720.
13. ^ Kils, U.: Swimming and feeding of Antarctic Krill, Euphausia superba - some outstanding energetics and dynamics - some unique morphological details. In Berichte zur Polarforschung, Alfred Wegener Plant for Polar and Marine Inquiry, Special Consequence iv (1983): "On the biology of Krill Euphausia superba", Proceedings of the Seminar and Report of Krill Ecology Group, Editor S. B. Schnack, 130-155 and championship page paradigm.
14. ^ Tortora, Gerard J.; Anagnostakos, Nicholas P. (1987). Principles of beefcake and physiology (Fifth ed.). New York: Harper & Row, Publishers. pp. 556–582. ISBN978-0-06-350729-6.
15. ^ Williams, Peter L; Warwick, Roger; Dyson, Mary; Bannister, Lawrence H. (1989). Gray's Anatomy (Thirty-7th ed.). Edinburgh: Churchill Livingstone. pp. 1278–1282. ISBN0443-041776.
16. ^ Romer, Alfred Sherwood; Parsons, Thomas S. (1977). The Vertebrate Body. Philadelphia, PA: Holt-Saunders International. pp. 349–353. ISBN978-0-03-910284-5.
17. ^ Krause J. William (July 2005). Krause'due south Essential Human being Histology for Medical Students. Universal-Publishers. pp. 37–. ISBN978-1-58112-468-2 . Retrieved 25 November 2010.
18. ^ Meiri, Due south.; Dayan, T. (2003-03-20). "On the validity of Bergmann's dominion". Journal of Biogeography. xxx (3): 331–351. doi:10.1046/j.1365-2699.2003.00837.x.
19. ^ Ashton, Kyle G.; Tracy, Mark C.; Queiroz, Alan de (Oct 2000). "Is Bergmann'due south Rule Valid for Mammals?". The American Naturalist. 156 (iv): 390–415. doi:10.1086/303400. JSTOR ten.1086/303400. PMID 29592141. S2CID 205983729.
20. ^ Millien, Virginie; Lyons, S. Kathleen; Olson, Link; et al. (May 23, 2006). "Ecotypic variation in the context of global climate alter: Revisiting the rules". Ecology Messages. 9 (7): 853–869. doi:10.1111/j.1461-0248.2006.00928.x. PMID 16796576.
21. ^ Fitzpatrick, Katie (2005). "Gigantothermy". Davidson Higher. Archived from the original on 2012-06-xxx. Retrieved 2011-12-21 .
22. ^ "Marsquake! NASA's InSight Lander Feels Its 1st Red Planet Tremor". Space.com. 23 Apr 2019.
23. ^ "Archived copy" (PDF). Archived from the original (PDF) on 2018-06-13. Retrieved 2018-08-22 . {{cite web}}: CS1 maint: archived copy equally title (link)

External links [edit]

• Sizes of Organisms: The Surface Surface area:Book Ratio Archived 2017-08-14 at the Wayback Car
• National Wildfire Coordinating Group: Surface Area to Volume Ratio
• Previous link non working, references are in this document, PDF

Further reading [edit]

• On Existence the Correct Size, J.B.S. Haldane Archived 2011-08-22 at the Wayback Machine

Source: https://en.wikipedia.org/wiki/Surface-area-to-volume_ratio

Posted by: steinhoffcoth1963.blogspot.com

Share this post